DOCUMENTS DE TRAVAIL : ONDES STATIONNAIRES.

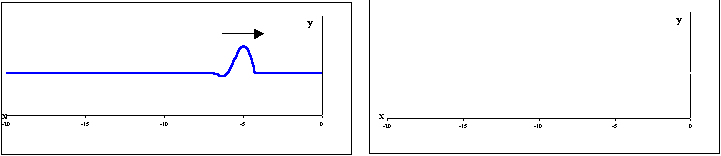
1. Ondes “ impulsion ” incidente et réfléchie sur un obstacle fixe (réflexion sans perte d’énergie).

Conclusion : l’onde …………………… est …… …………… forme que l’onde incidente, mais est ……………….. . Elle se propage à la même …………………… mais dans le sens ………………………………….

Remarque : si l’extrémité sur laquelle l’onde se réfléchit est ouverte, alors, l’onde réfléchie …………………………………………

2. ondes progressives sinusoïdales incidente et réfléchie sur un obstacle fixe.

a. Simulation d’un onde incident sinusoïdale se propageant sur une corde et arrivant sur un obstacle fixe.

Indiquer sur ces schémas, la longueur d’onde l et la période T.

b. Établissement d’un régime d’onde stationnaire.

Indiquer sur ces schémas, la longueur d’onde l et la période T.

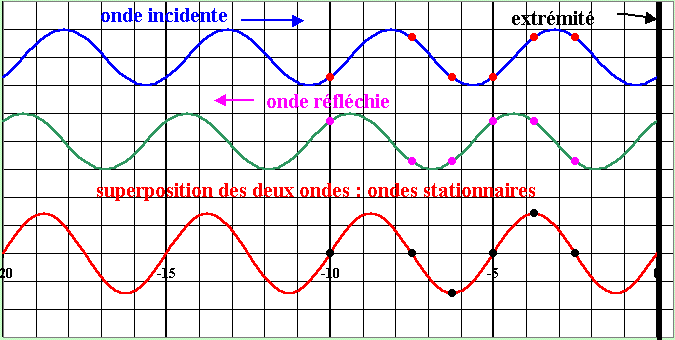
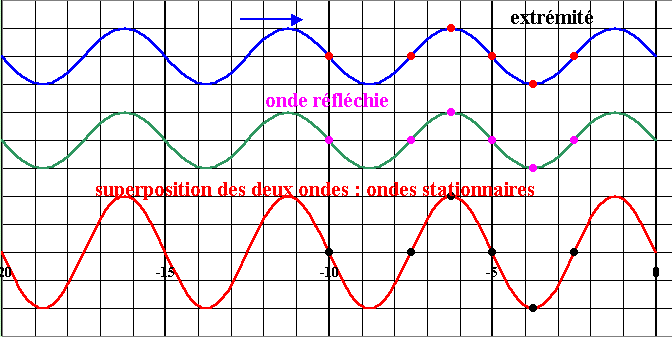
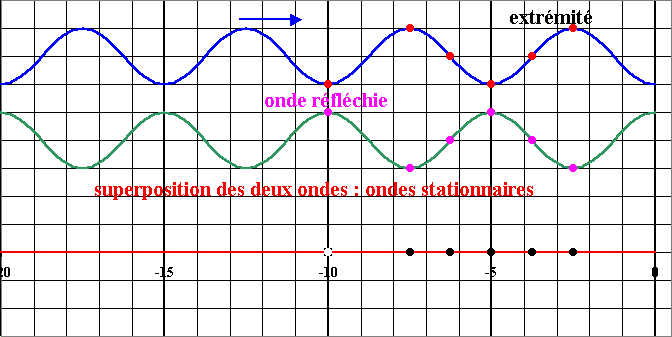
L'onde réfléchie est aussi …………………………… mais se déplace en sens ……………………………..

L’onde stationnaire est la résultante (superposition) de …………………….……………….. et de ……………………………………………..

• Certains points ne vibrent pas : ce sont les ………………………………….. . En ces points, les élongations des ondes incidentes et réfléchies sont …………………………………………. Deux nœuds consécutifs sont distants de ……………. Le point d’ancrage sur l’obstacle fixe est obligatoirement un …………………..

• D’autres points ont des amplitudes très grandes : ce sont les ………….. ……………. ………………….. En ces points, les élongations des ondes incidentes et réfléchies sont …………………………………………. Deux ventres consécutifs sont distants de ……………

Il n’y a plus …………………..……….. de la perturbation le long de la corde. L’amplitude de l’onde stationnaire étant plus grande que celle de l’onde incidente, il y a donc un phénomène de résonance.

• Quand les ondes stationnaires sont d'amplitudes maximales, les ondes incidente et réfléchie sont en ..............

• Quand les ondes stationnaires sont d'amplitudes minimales, les ondes incidente et réfléchie sont en ..............

Mode fondamental mode 1 : f₁ =

Harmonique mode 2 : f₂ =

Harmonique mode 3 : f₃ =

On en déduit que où n est un entier positif.

La longueur de la corde doit être un multiple de la ……………………………………….. pour que une onde stationnaire s’établisse.

Les deux extrémités fixes sont des ………………………..

• Condition d’établissement des ondes stationnaires

Pour que le système d’onde stationnaire soit établi, toutes les ondes qui se propagent dans le même sens doivent arriver …………………………. au point considéré car sinon les ondes se “ détruisent ” mutuellement. Le décalage entre deux ondes consécutives qui se propagent dans le même sens est dû à la durée d’un aller-retour effectué après ……….. réflexions sur des obstacles fixes.

La durée d’un parcours aller et retour est Dt =

Pour que deux ondes consécutives soient en phase, il faut : Dt = soit Et donc f = .

Retrouver la relation trouvée précédemment :

• En utilisant la relation trouvée la semaine dernière (f_n =. ), déterminer l’expression de la célérité d’une onde mécanique transversale dans une corde de masse linéique m et soumise à une tension T.

3. Ondes stationnaires le long d’une colonne d’air soumise à une vibration longitudinal sinusoïdale.

a. Observation des fréquences de vibration d’une colonne d’air soumise à des vibrations sonores sinusoïdale données par un haut parleur.

Observation : Pour certaines fréquences, l’intensité sonore est ……………………….. . La colonne d’air est alors en ……… ……………………………….

La relation reliant ces fréquence est ………………………………..

• Une onde longitudinale peut être simulée à l’aide d’un ressort. On observe alors pour certaines fréquences des …………………… et des ……………………………. caractéristiques d’une onde ……………………………….. Les extrémités du ressort sont des ……………………….. 

• On soumet cette colonne à une onde de fréquence environ 710 Hz correspondant à l’harmonique de mode 3. On déplace un micro à l’intérieur de cette colonne et on constate que l’amplitude du signal délivré présente des ………………………… et des ………………………… correspondant à des …………………………… et …………………………..  d’une onde stationnaire.

Les extrémités des tuyaux sont des ………………………………… contrairement au ressort. En effet, l’extrémité de la colonne est “ libre ” alors qu’elle serait fixe si la colonne était fermée. Observer la simulation d’une onde stationnaire sur une corde dont l’extrémité est libre.

• Observer la simulation des ondes stationnaires sonores dans un tuyau ouvert.

  

Remarque : On constate alors que dans un volume V encadrant un nœud de vibration, il y a plus de “ molécules d’air ” que dans le même volume encadrant un ventre de vibration. Que peut-on dire de la pression à l’intérieur de ces deux volumes ? On en déduit donc qu’un nœud de vibration correspond à un ………………….. de pression alors qu’un ventre de vibration correspond à un ………………………… de pression.

• Les valeurs des fréquences de résonance dépendent de …….………………………………………………….. Plus le tuyau est court et plus la fréquence du fondamental est …………………………………..

b. Répartition des ventres et des nœuds.

Conclusion : Si la colonne d’air est ouverte, il existe une relation entre la longueur L de la colonne et la longueur d’onde.

On a L = …………